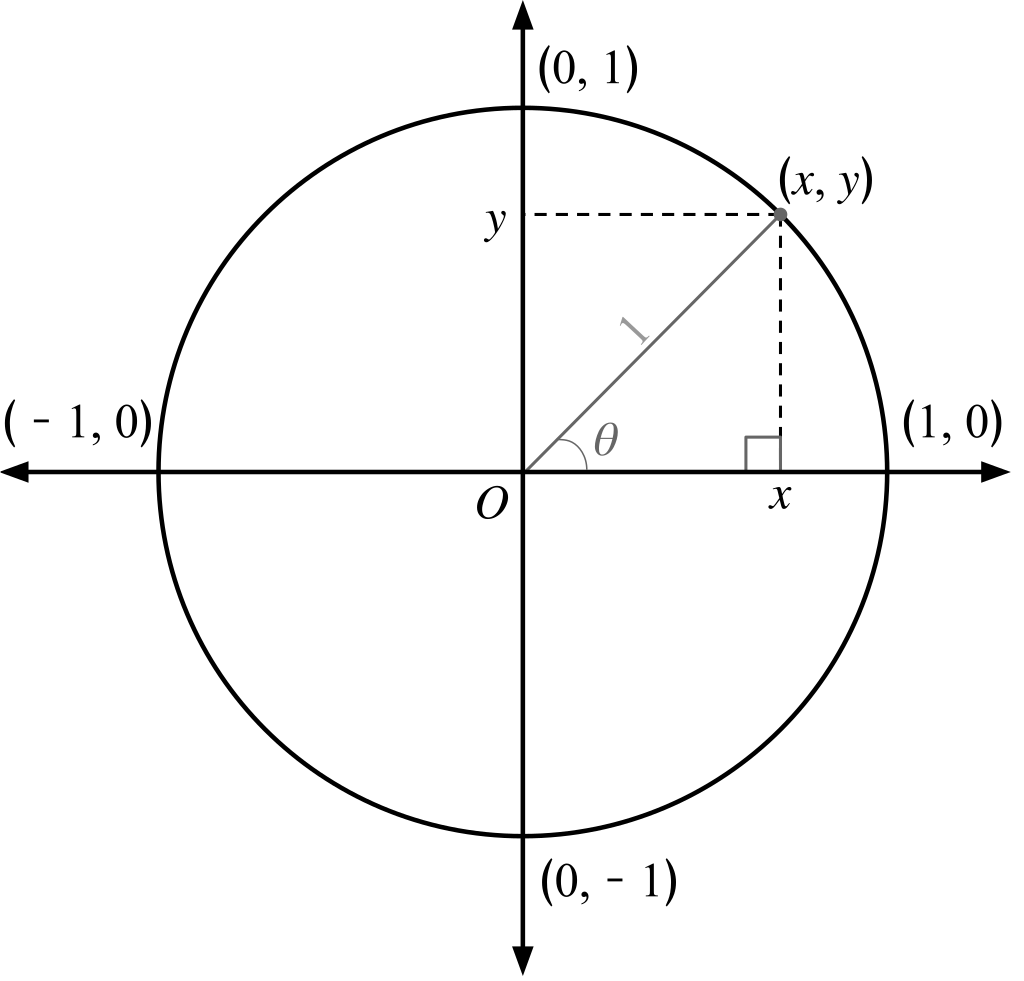
Unit Circle Definition:
A circle centered at the origin (0, 0)
It has radius of 1 unit.
Unit circle equation:
x2 + y2 = 1
Circle Equation:
Center at (a, b) and radius length r(x - a)2 + (y - b)2 = r2
Unit Circle Conversion:
(x, y) with a center (0, 0) and radius = 1(x - 0)2 + (y - 0)2 = 12
x2 + y2 = 1
Trigonometry Uses:
With radius = 1, we can do this:trignometry measurements like sin, cos, and tan
sin measurement for θ on the unit circle:
| sin(θ) = | Opposite Side of θ |
| Hypotenuse |
| sin(θ) = | y |
| 1 |
sin(θ) = y
cos measurement for θ on the unit circle:
| cos(θ) = | Adjacent Side of θ |
| Hypotenuse |
| sin(θ) = | x |
| 1 |
cos(θ) = x
tan measurement for θ on the unit circle:
| tan(θ) = | Opposite Side |
| Adjacent Side |
| tan(θ) = | y |
| x |
Or, tan(θ) is also known as
| tan(θ) = | sin(θ) |
| cos(θ) |
Trig Identity:
Recall above that x2 + y2 = 1Since x = cos(θ) and y = sin(θ):
cos2(θ) + sin2(θ) = 1
How does the What is a Unit Circle Calculator work?
Free What is a Unit Circle Calculator - This lesson walks you through what a unit circle is and how to use it
What 3 formulas are used for the What is a Unit Circle Calculator?
Unit Circle Origin = (0,0)
radius = 1
x2 + y2 = 1
radius = 1
x2 + y2 = 1
What 7 concepts are covered in the What is a Unit Circle Calculator?
- circle
- the set of all points in the plane that are a fixed distance from a fixed point
- equation
- a statement declaring two mathematical expressions are equal
- origin
- On a two digit coordinate plane, the point (0, 0), where the x-axis and y-axis cross.
- point
- an exact location in the space, and has no length, width, or thickness
- radius
- Distance from the center of a circle to the edge
C/2π - trigonometry
- Trigonometry studies relationships between side lengths and angles of triangles. The word trigonometry comes from the Greek word trigonon which means triangle and metron which means measure
- unit circle
- A circle centered at the origin (0, 0) with a radius of 1
x2 + y2 = 1