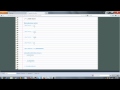
Given the hyperbola below
calculate the equation of the asymptotes
intercepts, foci points
eccentricity and other items.
| y2 | |
| 100 |
| - |
| x2 | |
| 49 |
| = |
| 1 |
Determine transverse axis:
Since our first variable is y
the hyperbola has a vertical transverse axis
Determine the equation of the asymptotes:
a = √100
a = 10
b = √49
b = 7
Calculate asymptote 1:
| Asymptote 1 = | ax |
| b |
| Asymptote 1 = | 10x |
| 7 |
Calculate asymptote 2:
| Asymptote 2 = | -ax |
| b |
| Asymptote 2 = | -10x |
| 7 |
Determine y-intercepts:
y-intercepts = ±a
y-intercepts = ±10
y-intercepts =(0, 10) and (0, -10)
Determine the foci:
Our foci are at (0,c) and (0,-c) where
a2 + b2 = c2
Therefore, c = √a2 + b2
a = √102 + 72
c = √100 + 49
c = √149
c = 12.206555615734
Foci = (0,12.206555615734) and (0,-12.206555615734)
Calculate eccentricity ε
| ε = | c |
| a |
| ε = | 12.206555615734 |
| 10 |
ε = 1.2206555615734
Calculate latus rectum:
| Latus Rectum = | 2b2 |
| a |
| Latus Rectum = | 2(7)2 |
| 10 |
| Latus Rectum = | 2(49) |
| 10 |
| Latus Rectum = | 98 |
| 10 |
Latus Rectum = 9.8
Calculate semi-latus rectum l:
| l = | Latus Rectum |
| 2 |
| l = | 9.8 |
| 2 |
l = 4.9
Final Answers:
hyperbola has a vertical
y-intercepts = (0, 10) and (0, -10)
Foci = (0,12.206555615734) and (0,-12.206555615734)
ε = 1.2206555615734
Latus Rectum = 9.8
l = 4.9
y-intercepts = (0, 10) and (0, -10)
Foci = (0,12.206555615734) and (0,-12.206555615734)
ε = 1.2206555615734
Latus Rectum = 9.8
l = 4.9


What is the Answer?
hyperbola has a vertical
y-intercepts = (0, 10) and (0, -10)
Foci = (0,12.206555615734) and (0,-12.206555615734)
ε = 1.2206555615734
Latus Rectum = 9.8
l = 4.9
y-intercepts = (0, 10) and (0, -10)
Foci = (0,12.206555615734) and (0,-12.206555615734)
ε = 1.2206555615734
Latus Rectum = 9.8
l = 4.9
How does the Hyperbola Calculator work?
Free Hyperbola Calculator - Given a hyperbola equation, this calculates:
* Equation of the asymptotes
* Intercepts
* Foci (focus) points
* Eccentricity ε
* Latus Rectum
* semi-latus rectum
This calculator has 1 input.
* Equation of the asymptotes
* Intercepts
* Foci (focus) points
* Eccentricity ε
* Latus Rectum
* semi-latus rectum
This calculator has 1 input.
What 2 formulas are used for the Hyperbola Calculator?
standard form of a hyperbola that opens sideways is (x - h)2 / a2 - (y - k)2 / b2 = 1
standard form of a hyperbola that opens up and down, it is (y - k)2 / a2 - (x - h)2 / b2 = 1
standard form of a hyperbola that opens up and down, it is (y - k)2 / a2 - (x - h)2 / b2 = 1
What 4 concepts are covered in the Hyperbola Calculator?
- asymptote
- a line that continually approaches a given curve but does not meet it at any finite distance
- foci
- special points with reference to which any of a variety of curves is constructed
- hyperbola
- conic section defined as the locus of all points in the plane the difference of whose distances and from two fixed points
- intercept