Consecutive Interior Angles Example:
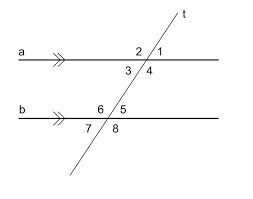
∠3 and ∠6 are consecutive interior angles
∠4 and ∠5 are consecutive interior angles
Properties:
They are supplementaryThey add up to 180°
Consecutive Interior Angles Proof:

Given: a || b and t with transversal t
Prove: ∠3 and ∠6 are supplementary
| Statement | Reason |
|---|---|
| a || b and t with transversal t | Given |
| ∠2 ≅ ∠6 | Corresponding Angle Postulate |
| m∠2 ≅ m∠6 | Definition of congruent angles |
| ∠3 and ∠2 are supplementary | Linear pair postulate |
| m∠3 + m∠2 = 180° | Definition of supplementary angles |
| m∠3 + m∠6 = 180° | Substitution Property |
| ∠3 and ∠6 are supplementary | Definition of supplementary angles |
How does the Consecutive Interior Angles Calculator work?
Free Consecutive Interior Angles Calculator - Shows you a proof of consecutive interior angles using parallel lines and a transversal
What 3 formulas are used for the Consecutive Interior Angles Calculator?
Consecutive interior angles are supplementary
Consecutive interior angles add up to 180°
Consecutive interior angles add up to 180°
What 7 concepts are covered in the Consecutive Interior Angles Calculator?
- consecutive interior angles
- the pairs of angles that are between two lines and on the same side of the line cutting through the two lines.
- interior angles
- the angles between adjacent sides of a rectilinear figure
- parallel lines
- two lines which never cross and always the same distance apart
- proof
- an inferential argument for a mathematical statement, showing that the stated assumptions logically guarantee the conclusion
- supplementary angles
- transversal
- a line that passes through two lines in the same plane at two distinct points.
- two column proof
- This consists of a list of statements, and the reasons that we know those statements are true. The two column proof has five parts:
1) Given
2) Proposition
3) Statement Column
4) Reason Column
5) Diagram